In this research direction, our efforts focused on developing new methods to model and optimize optical tomography systems including diffuse optical tomography and fluorescence tomography.
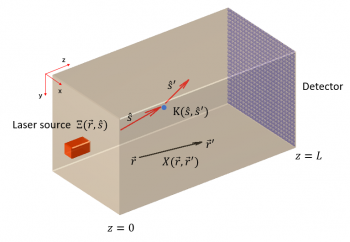
Diffuse optical imaging (DOI) is an emerging imaging modality where near-infrared light is used to probe the localized optical properties of a tissue. These properties generally vary between breast-cancer and normal tissue. Thus, DOI systems can be potentially used to diagnose breast cancer. However, given the high amount of scatter in the biological tissue with near-infrared light, there is an important need to optimize DOI system design that facilitates improved diagnosis. However, such optimization is complicated due to the non-availability of computationally efficient and accurate methods to model photon propagation, and the ill-posed nature of the image-reconstruction problem. To address the first issue, we developed a novel Neumann-series approach (Fig. 1). The approach overcame many issues suffered by the traditional diffusion-approximation-based methods. We then extended this method to non-uniform media, and implemented the algorithm on NVIDIA GPUs, which led to up to two orders of magnitude speedup compared to state-of-the-art non-GPU based systems.
Fig. 1: A schematic denoting the emission, scattering and attenuation of photons using mathematical operators. The Neumann series formalism we developed describes photon propagation in a scattering medium in terms of these operators.
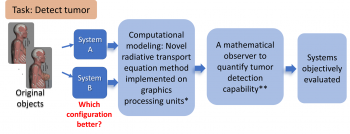
Next, we developed a novel Fisher-information-based mathematical observer that directly used the projection data (i.e. did not require reconstruction) to quantify the DOI system on the task of detecting a tumor with a high-absorption coefficient within the tissue. This observer was was implemented in conjunction with the Neumann-series approach and was shown to quantify the defect detection performance of DOI systems (Approach summarized in Fig. 2). Our research was one of the first investigations of objective assessment of image quality (OAIQ) in DOI and demonstrated that DOI systems could be quickly and accurately evaluated on simple tumor-detection tasks using the designed tools.
Fig. 2: Our OAIQ-based approach to optimize diffuse optical imaging systems
In another recent project, we have been developing reconstruction methods for fluorescence molecular tomography (FMT) for breast cancer detection.
References
- Y. Zhu, A. K. Jha*, D. F. Wong, A. Rahmim, “Image reconstruction in fluorescence molecular tomography with sparsity-initialized maximum-likelihood expectation maximization”, Biomed. Opt. Exp. 9(7), 3106-21, 2018 (link) (*Corresponding author)
- A. K. Jha, Y. Zhu, S, Arridge, D. F. Wong, and A. Rahmim, “Incorporating reflection boundary conditions in radiative transport equation-based photon propagation and image reconstruction in diffuse optical imaging”, Biomed. Opt. Express, 9(4), 2018.
- A. K. Jha, M. A. Kupinski, H. H. Barrett, E. Clarkson, J. H. Hartman, “A three-dimensional Neumann-series approach to model light transport in non-uniform media”, J. Opt. Soc. Amer. A, 29(8), 1885-99, 2012 PMCID: PMC3963433.
- A. K. Jha, M. A. Kupinski, T. Masumura, E. Clarkson, A. A. Maslov, H. H. Barrett, “Simulating photon transport in uniform media using the radiative transport equation: A study using the Neumann-series approach”, J. Opt. Soc. Amer. A, 29(8), 1741-1757, 2012. (Top 10 downloaded articles in Aug. 2012 edition.) PMCID: PMC3985394.
- A. K. Jha, E. Clarkson, and M. A. Kupinski, “An ideal-observer framework to investigate signal detectability in diffuse optical imaging”, Biomed. Opt. Express, 4(10), 2107-23, 2013 PMCID: PMC3799670.